Итак в статье я рассмотрю алгоритм 2d поворота обьекта. Как-то мне захотелось написать
простенькую гамесу, так просто, для души. В игре я сделал самолёт, он должен был летать =)
Тут то я и столкнулся с проблемой расчёта координат вершин поверхности самолёта. Поизвращавшись
с полчаса, я придумал простой, и на мой взгляд правильный алгоритм расчёта координат.
Итак, танцевать будем от того, что есть Центральная Точка (CP) и допустим 7 вершин у самолёта, из которых
он состоит (как полигон), а так же от главного поворота - текущее состояние обьекта. Итак, я думаю я вас
совсем заморочил, пожалуй, лучшим вариантом будет вот эта картинка
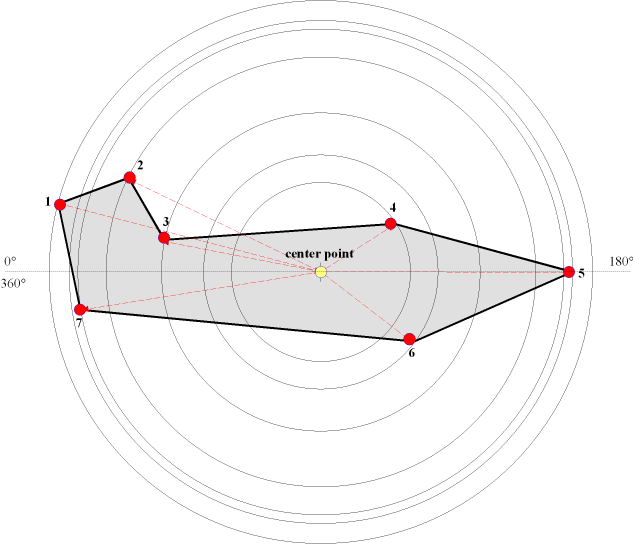
Итак, как же вычислить координаты всех точек имея CP и Угол Поворота (angle).
Для начала внимательней рассмотрим картинку и что мы имеем. Расстояние от CP до точки 1, это первое.
У нас есть угол поворота angle, например он равер 0, это два. Так же мы имеем угол, под которым находится расстояние от CP до 1 (angle1)
допустим оно равно у нас 10 градусам.
И у нас собственно есть сама координата CP.
Ну чтож, за работу!
Чтобы вычислить координату точки под текушим углом, нужен примерно такой алгоритм:
(координата X точки 1) = (координата X точки CP) + ((Расстояние от CP до точки 1) * косинус (((angle + angle1) * (число ПИ) / 360)))
(координата Y точки 1) = (координата Y точки CP) - ((Расстояние от CP до точки 1) * синус (((angle + angle1) * (число ПИ) / 360)))
Алгоритм на самом деле очень простой - мы просто вычисляем точку окружности с радиусом, равным длинне CP-точка1, и углом angle + angle1.
Это формула строится на элементарной математике. Вместо 360 кстати можно использовать и меньшие и большие велечина, в нашем случае -
360, я выбрал потому, что на школьном тран-спор-тире 360 делений =) Увеличив это число мы регулируем "шаг" - на сколько повернётся обьект,
я бы порекомендовал сделать эту величину поменьше, к примеру 180, если не надо большой точности, и напротив если она требуется, то увеличить этот
параметр, раза в два.
Ну и на последок я приведу пример процедуры высчитывающей координаты всех точек.
Процедура будет на дельфи, но я думаю переделать её под СИ или АССЕМБЛЕР не составит труда.
| Листинг 1.0 - процедура расчёта точек под заданным углом |
var // глобальные переменные
plane_pnts : array[1..7] of TPOINT; //количество вершин
plane_coord : TPOINT; // координаты самолёта (CP)
plane_tangage : integer; // наклон самолёта
plane_rgn
...
procedure DrawPlane(angle);
begin
plane_pnts[1].X := plane_coord.X +
round(18*cos((plane_tangage-10)*pi/180));
plane_pnts[1].Y := plane_coord.Y -
round(18*sin((plane_tangage-10)*pi/180));
plane_pnts[2].X := plane_coord.X +
round(23*cos((plane_tangage-25)*pi/180));
plane_pnts[2].Y := plane_coord.Y -
round(23*sin((plane_tangage-25)*pi/180));
plane_pnts[3].X := plane_coord.X +
round(20*cos((plane_tangage-40)*pi/180));
plane_pnts[3].Y := plane_coord.Y -
round(20*sin((plane_tangage-40)*pi/180));
plane_pnts[4].X := plane_coord.X +
round(5*cos((plane_tangage-30)*pi/180));
plane_pnts[4].Y := plane_coord.Y -
round(5*sin((plane_tangage-30)*pi/180));
plane_pnts[5].X := plane_coord.X +
round(15*cos((plane_tangage-150)*pi/180));
plane_pnts[5].Y := plane_coord.Y -
round(15*sin((plane_tangage-150)*pi/180));
plane_pnts[6].X := plane_coord.X +
round(30*cos((plane_tangage-180)*pi/180));
plane_pnts[6].Y := plane_coord.Y -
round(30*sin((plane_tangage-180)*pi/180));
plane_pnts[7].X := plane_coord.X +
round(20*cos((plane_tangage-220)*pi/180));
plane_pnts[7].Y := plane_coord.Y -
round(20*sin((plane_tangage-220)*pi/180));
plane_rgn := CreatePolygonRgn(plane_pnts, 8, ALTERNATE);
FillRect(dc, SkyRect, backg_brsh);
end;
|